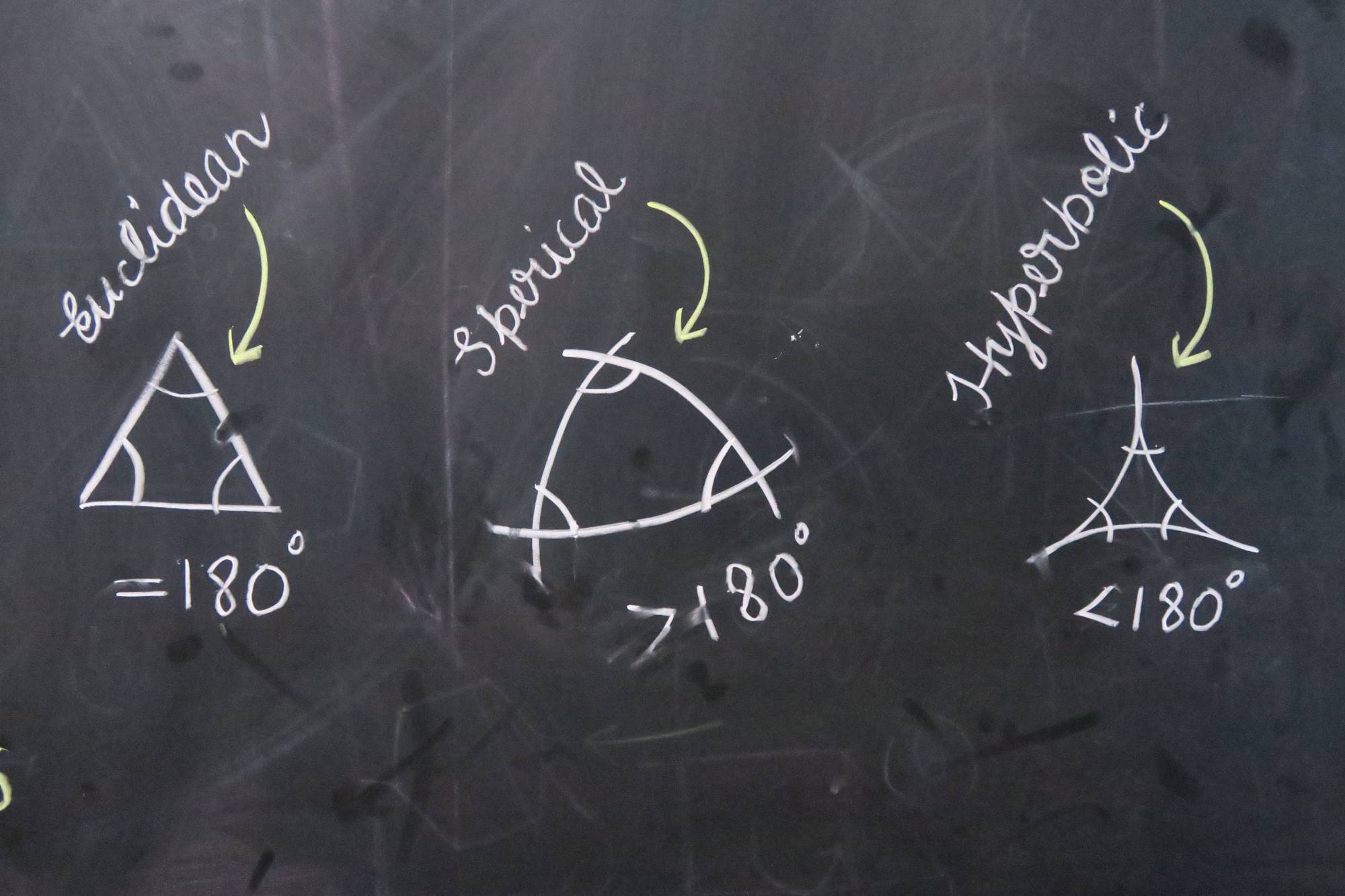We have built a world of rectilinearity. The rooms we live in, the skyscrapers we work in, the grid-like arrangements of our streets, speak to us in straight lines. Yet outside our boxes the natural world teems with swooping, curling and crenellated forms from the fluted surfaces of lettuce and fungi to the frilled skirts of nudibranchs and the animal undulations of sea slugs and corals. We have learned to play by Euclidean rules because two thousand years of geometrical training have engraved the grid in our minds. But in the early 19th century, mathematicians became aware of a space in which lines cavorted in aberrant formations, suggesting the existence of a new geometry.
To all at the time, hyperbolic space seemed pathological, for it contravened Euclid’s laws, overthrowing millennia of mathematical wisdom and offending common sense. “Fear it no less than the sensual passions; for it too may … deprive you or your health, piece of mind, and happiness in life” wrote Wolfgang Boylai, one of the pioneers of this new domain.
Characterized by an almost organic excess, hyperbolic surfaces resemble nothing so much as a sea creature. Indeed corals, kelps, sea sponges, and nudibranchs all display hyperbolic geometry in the surfaces of their being. Nature has a love affair with hyperbolic forms and has been experimenting with their possibilities for hundreds of mullions of years, especially in the sea. Wherever a creature would benefit from maximal surface area to gather nutrients, hyperbolic surfaces are an ideal solution, packing a large area into a small 3-D space. Corals and other filter feeding organisms have thus converged on an optimal geometric solution to the problem of lunch.
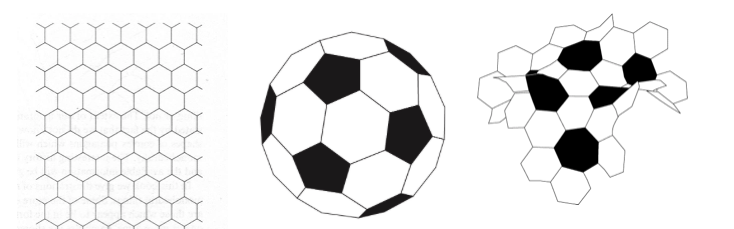
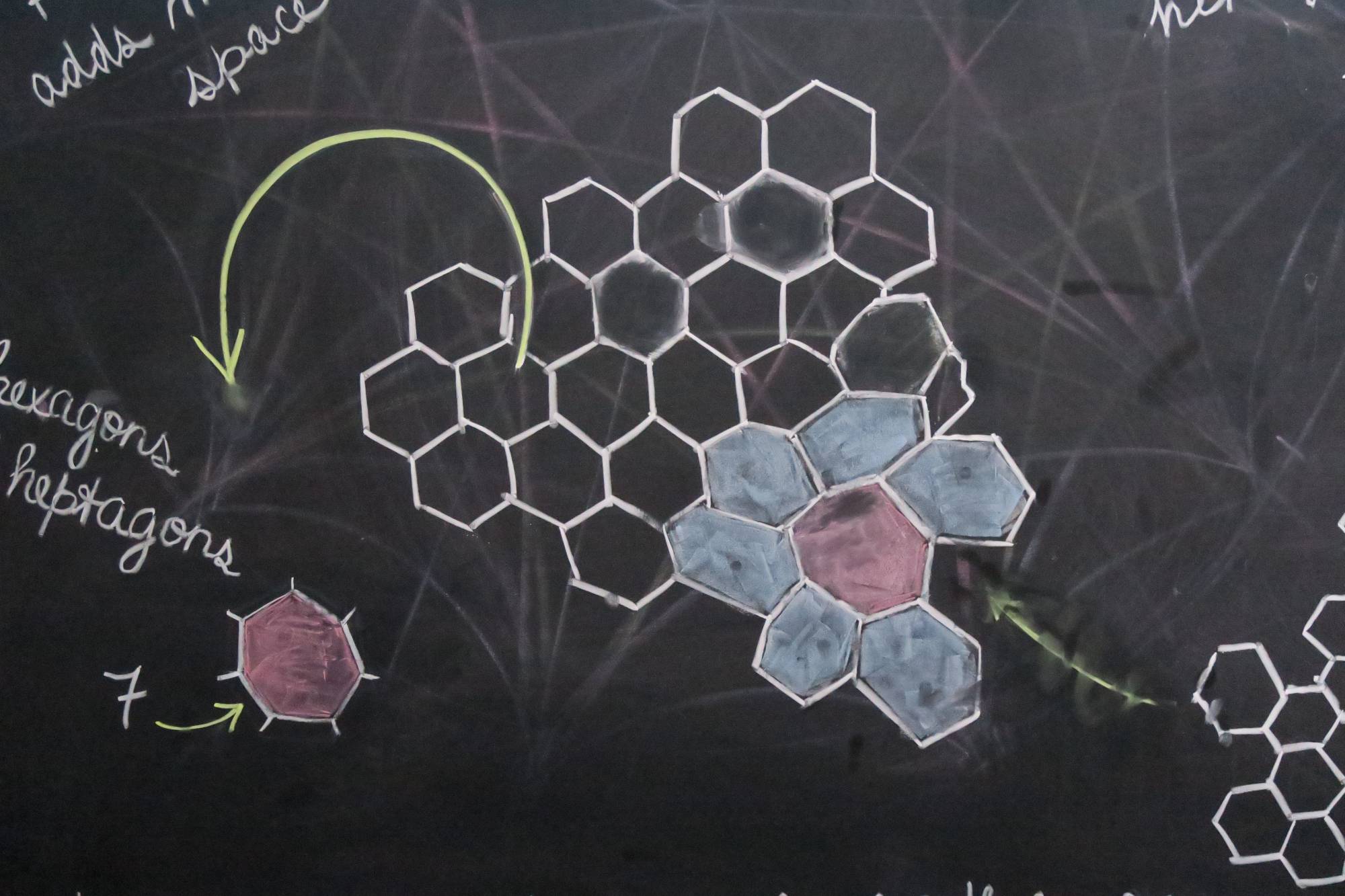
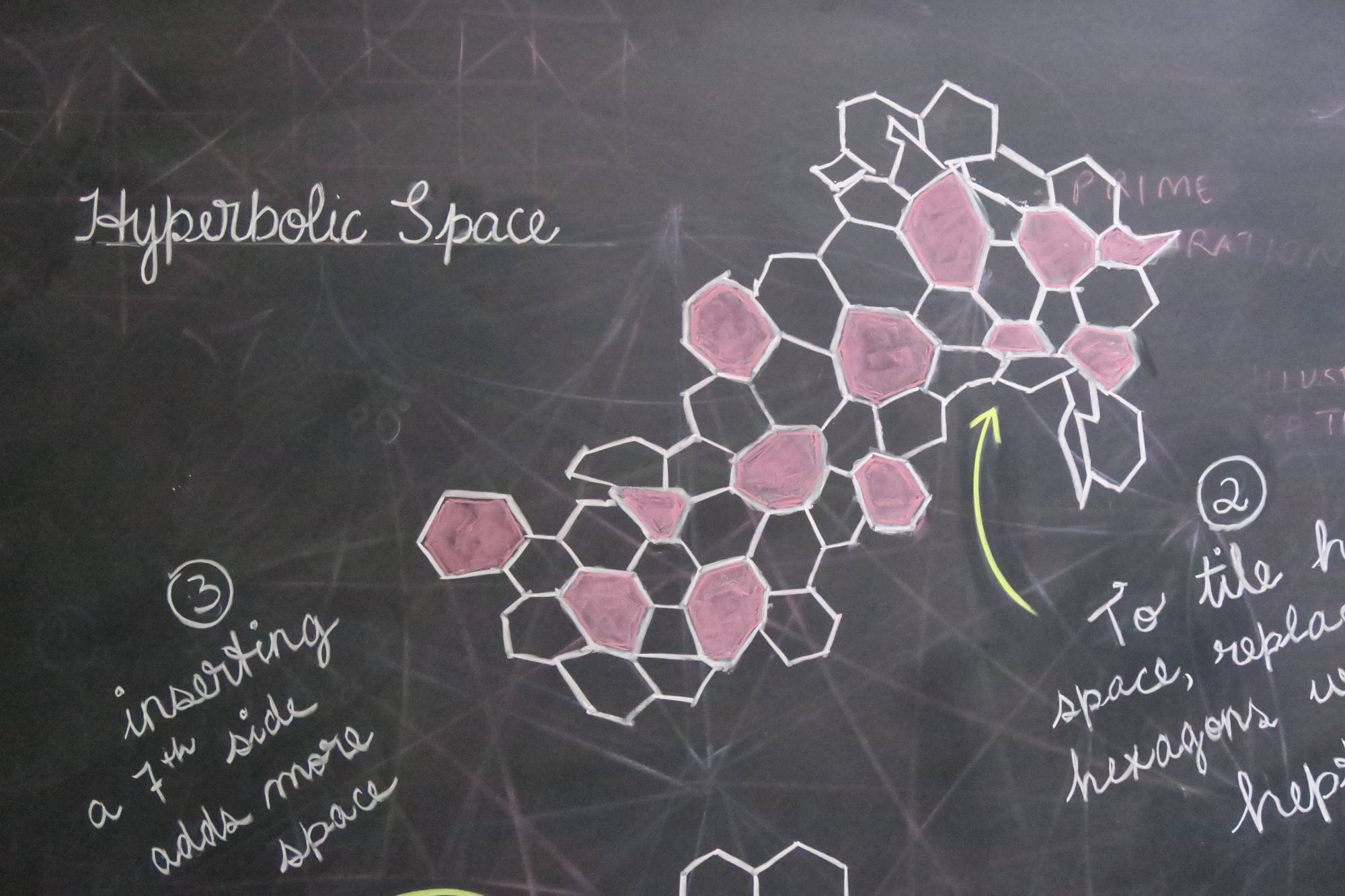
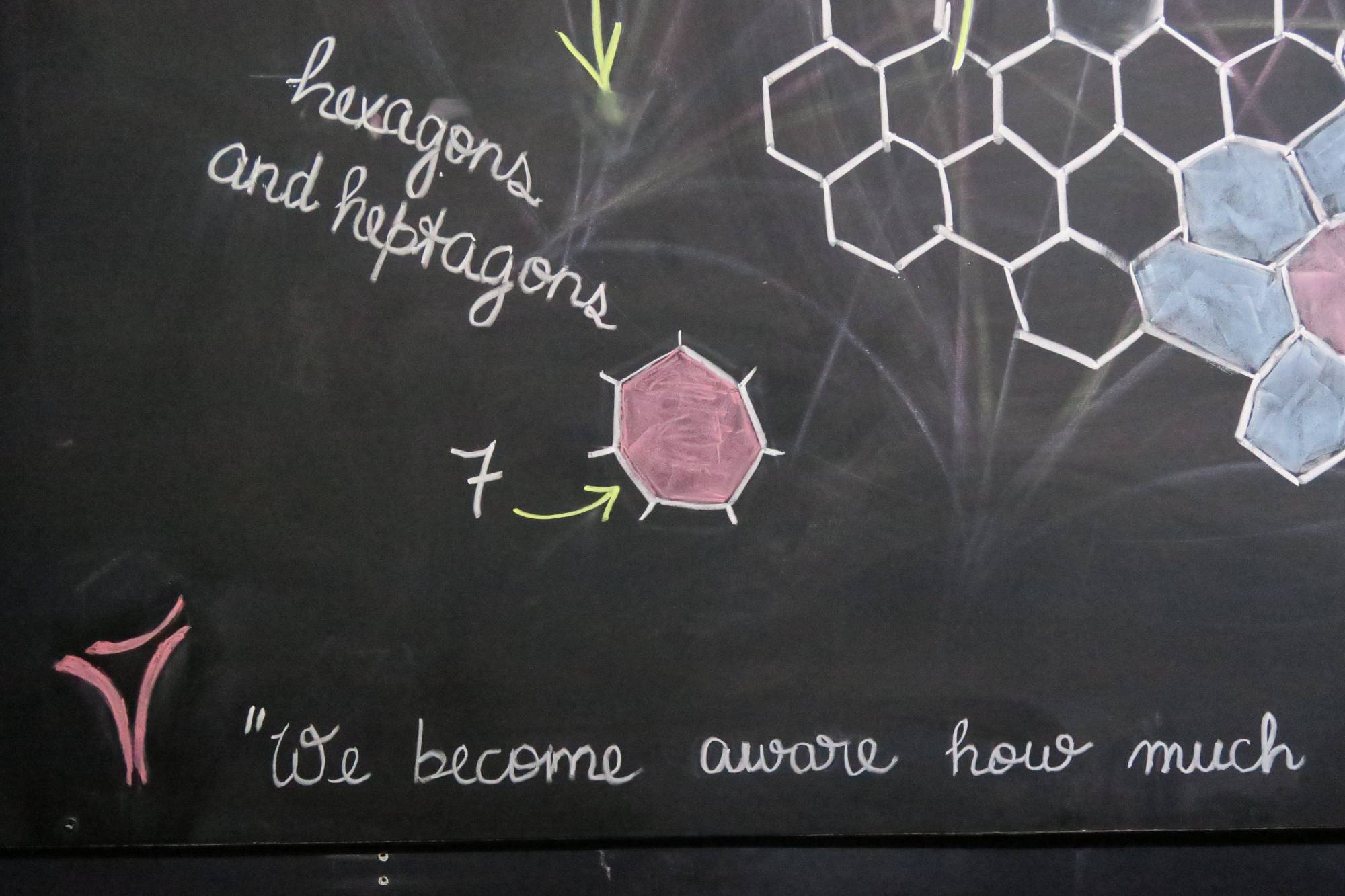
There are various way to characterize geometric surfaces. One is through tessellations, the way we can fill an area with polygons without any gaps. On a Euclidean surface we can fill the space with hexagons, the classic tiling pattern of bathroom floors. To cover the surface of a sphere, however, we must remove some of the six-sided hexagons replacing them with five-sided pentagons. By taking away sides, we reduce the surface area causing it to pull in on itself creating a closed space like a soccer ball. What happens if we make the opposite move? Now we replace some hexagons with seven-sided heptagons. Here we have added sides, thus increasing surface area, as on a lettuce leaf. The resulting form is, technically, the geometric opposite or a sphere.
Mathematicians characterize the Euclidean plane as a surface of zero curvature, a sphere as a surface of positive curvature, and the hyperbolic plane as a surface of negative curvature – thus making it a geometric analog of a negative number.
Another way of describing these three geometries is through the behavior of parallel lines. On a Euclidean surface parallel lines stay the same distance apart forever. On a spherical surface, however, parallel lines converge. Think of how the lines of longitude on the surface of the Earth – which all cross the equator parallel to one another –converge at the North and South poles. Reciprocally, on a hyperbolic surface, parallel lines can diverge. These, so-called, ultraparallels are an index of excess that nearly drove mathematicians mad when their existence was first intuited.
Grasping the formalities of hyperbolic geometry is a task that taxed the best minds in mathematics for nearly 2000 years, and continues to challenge math majors at universities the world over. How does one understand “negative curvature space”? In 1993 Dr. Daina Taimina at Cornell University gave us a powerful pedagogical tool which finally enabled mathematicians, and others, to see hyperbolic forms. The method she used was crochet. With a ball of yarn and a crochet hook we can construct hyperbolic surfaces by following the simple algorithm: “Crochet ’n’ stitches, increase one; repeat ad infinitum.” By adding stitches, just as in the models above we added in sides, we increase the surface area and generate a tactile model of this verboten geometry.
To learn more about these geometric surfaces and hyperbolic space see the Institute For Figuring’s online exhibit.
In exhibitions of the Crochet Coral Reef, we sometimes feature a Mathematics Blackboard, a large-scale site-specific drawing that poetically diagrams these surfaces and the principles underlying them.
The Mathematics Blackboard has been exhibited at the Williamson Gallery, Art Center College of Design (2012), and at the 2019 Venice Biennale. The Biennale installation was generously sponsored by the Australian Mathematical Sciences Institute (AMSI). Special thanks to AMSI director, Tim Brown; and to drawing assistant Richard Nielsen.